- 7 Marks
Question
A TV manufacturer finds that he can sell xx units per week at a price p=250−0.5xp = 250 – 0.5x each. His cost of production of xx TV sets per week is given by C=240+2xC = 240 + 2x.
Required:
(i) Determine how many sets per week he should produce to maximize his profit. (5 Marks)
(ii) Determine the maximum profit. (2 Marks)
Answer
Given that :
Demand function: 250 – 0.5x
Cost function: 240 + 
(i) Profit Function:
The profit maximizing quantity is given by
Therefore we have X = 83.33
(ii) Maximum Profit:
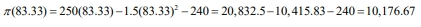
- Tags: Marginal Cost, Marginal Revenue, Production, Profit Maximization, TV Sets
- Level: Level 1
- Topic: Elements of Calculus
- Series: NOV 2015
- Uploader: Kwame Aikins