- 40 Marks
Question
The Managing Director of NTAMS Manufacturing Company Limited, located in Lagos, attended a seminar titled “Optimizing scarce resource utility in a manufacturing setting with particular reference to linear programming.” Upon his return, he initiated a management meeting to discuss key insights, prompted by the board’s decision to prioritize two primary products.
The following are cost data for the anticipated products “Biggi” and “Smalli”:
| Costs | Biggi (₦) | Smalli (₦) |
|---|---|---|
| Material Costs | (5kg @ ₦50/kg) 250 | (3kg @ ₦50/kg) 150 |
| Labour Costs: | ||
| Machining Time | (4 hours @ ₦15/hr) 60 | (2 hours @ ₦15/hr) 30 |
| Processing Time | (4 hours @ ₦10/hr) 40 | (5 hours @ ₦10/hr) 50 |
The company adheres to a pricing policy where total cost of production is marked up by 20%. Annual overhead is ₦10,000,000, allocated on a 3:2 basis between Biggi and Smalli, with a projected production of 200,000 Biggis and 100,000 Smallis.
Available resources for the upcoming year:
- Materials: 1,800,000 kg
- Machine Time: 800,000 hours
- Other Processing Time: 1,400,000 hours
Required:
As the management accountant:
- Explain briefly the concept of linear programming and its usefulness.
(5 Marks) - Compute the Prices for Biggi and Smalli using the company’s pricing policy.
(5 Marks) - Advise the company on the output levels needed to maximize total profit, with full financial analysis support.
(10 Marks) - Explain the meaning and limitations of “shadow prices” and calculate them for constraints.
(12 Marks) - Assuming consistent conditions for three years with an investment cost of ₦45,000,000 and a 15% cost of capital:
- Determine if this venture is justified.
(4 Marks) - Find the breakeven discount factor for this project.
(4 Marks)
- Determine if this venture is justified.
Answer
a. Concept of Linear Programming and Usefulness
Linear programming is a mathematical technique used to determine the best outcome (like maximizing profit or minimizing cost) within a set of constraints. A linear programming problem typically involves maximizing or minimizing a linear objective function subject to linear constraints. Both the constraints and the objective are represented by linear equations or inequalities.
Usefulness of Linear Programming:
- Budgeting: Linear programming can be used to identify the most profitable use of resources when there is more than one limiting factor.
- Capital Budgeting: It helps allocate limited funds optimally among competing projects in cases of multi-period capital rationing.
- Transfer Pricing: In a divisionalized organization, linear programming can compute optimal transfer prices when supply capacity is limited.
- Relevant Cost Calculation: Linear programming can establish the opportunity cost when more than one scarce resource exists.
- Control: It is also useful in variance analysis; for example, adverse material usage variances can indicate material wastage, valued at standard cost plus opportunity cost
b. Computation of Unit Selling Price and Associated Unit Profit for Biggis and Smallis
| Biggis (₦) | Smallis (₦) | |
|---|---|---|
| Material | 250 | 150 |
| Labour (Machine) | 60 | 30 |
| Labour (Processing) | 40 | 50 |
| Overhead | 30 | 40 |
| Total Costs | 380 | 270 |
| Profit per unit | 76 | 54 |
| Selling Price | 456 | 324 |
c. ADVICE ON THE OUTPUT TO BE PRODUCED TO MAXIMISE TOTAL PROFIT
STEP 1 –DETERMINATION OF LIMITING FACTOR
Materials needed to produce 200,000 units of Biggis & 100,000 units of Smallis

Conclusion:
Materials are not limiting factor since available resources exceed
resources needed to meet production levels.
Machine time needed to produce 200,000 units of Biggis and 100,000 units of Smallis
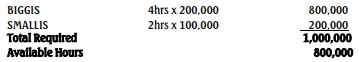
Conclusion:
Machine time is a limiting factor since hours available are less than
the hours needed to meet production levels.
Other processing time needed to produce 200,00 units of Biggs and
100,000 units of smallis:
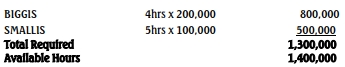
Conclusion:
Other processing time is not a limiting factor since hours available
exceeds hours needed to meet production levels.
Step 2: Priority of Production Plan
| Biggis | Smallis | |
|---|---|---|
| Selling Price | 456 | 324 |
| Variable Costs | 350 | 230 |
| Contribution | 106 | 94 |
| Machine Time | 4 | 2 |
| Contribution/Unit of Machine Time | 26.5 | 47 |
| Ranking | 2nd | 1st |

Conclusion: NTAMS should produce 100,000 units of Smallis and 150,000 units of Biggis for maximum profit
d. Shadow Prices
i. SHADOW PRICE
The shadow price is the increase or decrease in the objective function’s value per unit increase or decrease in a binding constraint. It is also known as the dual price.
- Usefulness: Shadow prices help determine the relevant cost of scarce resources, set transfer prices, and allocate funds when there is multi-period capital rationing.
- Limitation: Shadow prices are only valid within a limited output range. For example, shadow prices may reduce to zero as more of the limiting factor (e.g., labor hours) is supplied.
ii. CALCULATION OF SHADOW PRICE OF THE CONSTRAINTS
Shadow price only exists for binding resources – hence shadow price
will only exist for machine time. If one (1) additional machine time is
available, total machine time will be 800,001
Total units of Biggis to be produced wil l be 150,000.25 units (600,001/4)
New Total contribution will be (100,000 x 94) + (150,000.25 x 106) =
25,300,026.50
Previous total contribution was (100,000 x 94) + (150,000 x 106) =
25,300,000
Increase in contribution = 25,300,026.50 – 25,300,000 = 26.50
e. i
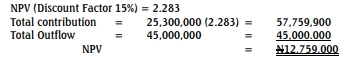
Yes, the project‟s NPV is positive and therefore worthwhile
ii)
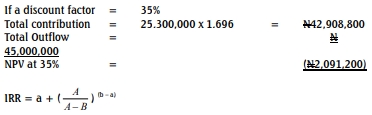

- Tags: Costing, Decision Making, Linear Programming, Resource Optimization, Scarce Resources
- Level: Level 2
- Topic: Costing Systems and Techniques
- Series: MAY 2021
- Uploader: Kwame Aikins
