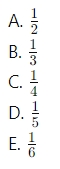Question Tag: Probability

Search 500 + past questions and counting.

  • Filter by Professional Bodies

  • Filter by Subject

  • Filter by Series

  • Filter by Topics

  • Filter by Levels

  • 10 Marks

QTB – May 2017 – L1 – SB – Q4b – Operations Research

Identify non-basic variables in a transportation model and calculate the probability of a specific event in random disk selection.

i. Given the following initial basic tableau of a transportation problem:

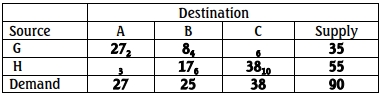
Identify the non-basic variables and compute their corresponding
relative cost coefficients. (4marks)

ii. A bag contains 39,800 white disks and 200 black disks from which
1,000 disks are taken at random. Calculate the probability that the
sample contains 4 black disks. (6marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SB – Q4b – Operations Research"

  • 10 Marks

QTB – May 2017 – L1 – SB – Q4a – Statistics

Calculate the proportion of damaged blocks and the probability of taking a damaged block from a specific lorry using a tree diagram.

a. A fleet of lorries A, B, and C are loaded with blocks meant for a building site.
Lorry A carries 2/5 of all the needed blocks, B carries 3/4 of what lorry A carries, and lorry C carries the rest. Lorries A, B, and C contain 13%, 15%, and 11% damaged blocks, respectively.

By drawing a suitable tree diagram, calculate:
i. The proportion of damaged blocks in the fleet. (8 Marks)

ii. The probability of randomly taking a damaged block from lorry B. (2 Marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SB – Q4a – Statistics"

  • 10 Marks

QTB – May 2017 – L1 – SB – Q2a – Statistics

Probability calculations for dice roll and random sampling in block production.

i. A six-sided and fair die is thrown into the air. What is the probability:

  • Of NOT getting a SIX?
  • That either a THREE, a FOUR, or a FIVE will fall uppermost?
  • Of obtaining an even number?
    (5 Marks)

ii. A block-making factory produces TWO types of blocks: 6-inch and 9-inch. ONE quarter of its output on a particular day are 6-inch blocks, while the remaining three-quarters are 9-inch blocks. If samples of 3 are taken at random, what is the probability of obtaining:

  • One 6-inch block?
  • Two 6-inch blocks?
  • One or two 6-inch blocks?
    (5 Marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SB – Q2a – Statistics"

  • 1 Marks

QTB – May 2017 – L1 – SA – Q16 – Statistics

This question asks to identify a false statement about normal distribution.

Which of the following is NOT TRUE about Normal Distribution?
A. Normal distribution is a frequency distribution.
B. Both tails of the distribution approach but never meet the horizontal axis.
C. It is a probability distribution of a continuous variable that fits many naturally occurring distributions.
D. The exact shape of the normal curve depends on the mean of the distribution.
E. The area under the normal curve represents the probability and totals 1 or 100%.

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SA – Q16 – Statistics"

  • 1 Marks

QTB – May 2017 – L1 – SA – Q15 – Statistics

This question involves calculating the probability that a defective item is from process B.

A large batch of components of TV sets is stocked by a company. The batch comprises components that are manufactured by processes A, B, and C. There are twice as many components from process A as from each of processes B and C in a batch. Components from A contain 8% defectives, and those from B and C contain 11% and 14% defectives respectively.
The probability that a defective item is from process B is:
A. 0.228
B. 0.238
C. 0.248
D. 0.258
E. 0.268

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SA – Q15 – Statistics"

  • 1 Marks

QTB – May 2017 – L1 – SA – Q13 – Statistics

This question calculates the probability of rolling either a four or a six on a six-sided die.

A six-sided die is thrown into the air, the probability that either a FOUR or a SIX will fall upper most is:

 

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2017 – L1 – SA – Q13 – Statistics"

  • 1 Marks

QTB – Nov 2014 – L1 – SA – Q3 – Probability

Determines the probability that daily sales exceed a specified value, given a normal distribution with known mean and standard deviation.

The daily sales figures of a supermarket follow a normal distribution with a mean of N60,000 and a standard deviation of N14,000. Find the probability that the sales figure of a certain day exceeds N46,000.
A. 0.1587
B. 0.1590
C. 0.8413
D. 0.8415
E. 0.8423

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – Nov 2014 – L1 – SA – Q3 – Probability"

  • 1 Marks

QTB – Nov 2014 – L1 – SA – Q2 – Probability

Determines the probability that a customer does not receive a mutilated note from the cashiers.

The following tree diagram shows the scenario with two paying cashiers (C1 and C2) at a Microfinance Bank where M represents mutilated notes and N represents new notes:

he probability that a customer of the bank does not receive a mutilated note is:
A. 0.1125
B. 0.8725
C. 0.8875
D. 0.8525
E. 0.8850

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – Nov 2014 – L1 – SA – Q2 – Probability"

  • 1 Marks

QTB – Nov 2014 – L1 – SA – Q1 – Probability

Determines the correct definition of mutually exclusive events.

Two events are said to be mutually exclusive if
A. The occurrence (or non-occurrence) of one event does not affect the occurrence (or non-occurrence) of the other event
B. Both events can occur simultaneously
C. The occurrence of one event precludes the occurrence of the other event
D. Both are impossible events

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – Nov 2014 – L1 – SA – Q1 – Probability"

  • 10 Marks

QTB – May 2016 – L1 – SB – Q5b – Statistics

This question involves calculating the probability of a bag of Pando Yam weighing less than a specified value using the normal distribution.

The weights of bags of Pando Yam produced by Swallow Company Limited are normally distributed with a mean of 3,020 grams and a standard deviation of 4 grams.

Required:
i. If a bag is picked at random, what is the probability that it weighs:

  • Less than 3,012 grams? (4 marks)
    ii. Between 3,012 grams and 3,021.6 grams? (6 marks)
    Show all the relevant normal distribution diagrams.

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QTB – May 2016 – L1 – SB – Q5b – Statistics"

  • 20 Marks

QT – May 2016 – L1 – Q3 – Probability

Calculate the probabilities of various outcomes in a card drawing scenario, including conditional probability based on drawing a red card.

a) If from a normal pack of 52 cards, consisting of four suites each of 13 cards, one card is randomly selected:

Required:

Calculate the probabilities of selecting the following:

i) An ace
ii) A club
iii) An ace or a club
iv) The ace of clubs
v) A picture card (i.e. a jack, queen or king)
vi) A red card
vii) A red king
viii) A red picture card

b) Given that a card selected is red, calculate the probability that it is a picture card.

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2016 – L1 – Q3 – Probability"

  • 20 Marks

QT – Nov 2017 – L1 – Q5 – Probability

Use the normal distribution to compute probabilities related to loan default amounts.

The distribution of the total loan amounts defaulted by customers of a bank annually is approximated by a normal distribution. The average default amount is GH¢1.50 million, and the standard deviation is GH¢0.50 million.

Required:
a) Determine the probability that the total loan amount defaulted exceeds GH¢1.50 million. (3 marks)
b) Determine the probability that the total loan amount defaulted is between GH¢0.86 million and GH¢0.90 million. (4 marks)
c) Determine the probability that the total amount defaulted is at most GH¢2 million. (4 marks)
d) Determine the amount to be allowed per annum for loan defaults if 1% of actual defaults exceed this amount. (3 marks)
e) Determine the lower quartile of the distribution of total loan amounts defaulted. (3 marks)
f) Determine the upper quartile of the distribution of total loan amounts defaulted. (3 marks)
(Total: 20 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – Nov 2017 – L1 – Q5 – Probability"

  • 16 Marks

QT – May 2019 – L1 – Q6b – Probability

Calculate probabilities based on student survey data regarding their favorite sports.

A survey of The Institute of Chartered Accountants (Ghana) students asked the question: “What is your favourite sport?” The results are summarized below:

Level Football Boxing Hockey Total
1 68 41 46 155
2 84 56 70 210
3 59 74 47 180
Total 211 171 163 545

Required: i) What is the probability of selecting a student whose favourite sport is boxing? (2 marks)

ii) What is the probability of selecting a Level 1 student? (2 marks)

iii) If the student selected is a Level 2 student, what is the probability that the student prefers hockey? (3 marks)

iv) If the student selected is a Level 2 student, what is the probability that the student prefers football or hockey? (3 marks)

v) If the student selected prefers football, what is the probability that the student is a Level 1 student? (3 marks)

vi) If the student selected is a Level 3 student, what is the probability that the student prefers football, boxing, or hockey? (3 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2019 – L1 – Q6b – Probability"

  • 20 Marks

QT – May 2019 – L1 – Q4b – Probability

Solve problems involving normal distribution, life spans, and warranty calculation using Z-scores.

CarJoy Manufacturing Company produces electronic components that have life spans normally distributed with mean  hours and standard deviation σ hours. Only 1% of the components have a life span less than 3,500 hours and 2.5% have a life span greater than 5,500 hours.

Required:
i) By standardizing the values of  to the standard normal values, obtain TWO (2) linear equations in  and . (4 marks)

ii) Using an appropriate method of solving simultaneous equations, determine the value of  and  in (i) above. (4 marks)

iii) Determine the proportion of electronic components with life spans between 4,120.50 hours and 5,052.45 hours. (4 marks)

iv) If the company gives a warranty of 4,000 hours on the components, find the percentage of components the company is expected to replace under the warranty. (4 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2019 – L1 – Q4b – Probability"

  • 4 Marks

QT – May 2019 – L1 – Q4a – Probability

Sketch the normal distribution curve showing the mean, median, and mode.

The continuous random variable X is normally distributed with mean μ and variance σ2.

Required:
Sketch the distribution of  and indicate on your sketch the mean, median, and mode. (4 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2019 – L1 – Q4a – Probability"

  • 6.5 Marks

QT – May 2017 – L1 – Q6b – Probability

Determine the probabilities of specific outcomes when tossing three fair coins.

If three fair coins are tossed:

Required:

i) Determine the probability of getting two heads and a tail.
(3.5 marks)

ii) Determine the probability of getting three tails.
(3 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2017 – L1 – Q6b – Probability"

  • 13.5 Marks

QT – May 2017 – L1 – Q6a – Probability

Calculate probabilities from a tree diagram based on people's chocolate preferences and eye color.

Consider people’s preferences in terms of chocolate and their eye color, presented as a probability tree diagram below:

  • 30% of people have brown eyes, 40% have green eyes, and the remaining have blue eyes.
  • 70% prefer milk chocolate, 10% prefer white chocolate, and the remaining prefer plain chocolate.

Using the tree diagram above, calculate the probability that a person:

i) Prefers plain chocolate and has brown eyes.
(1.5 marks)

ii) Prefers milk chocolate and has brown eyes.
(1.5 marks)

iii) Prefers white chocolate and has brown eyes.
(1.5 marks)

iv) Prefers plain chocolate and has green eyes.
(1.5 marks)

v) Prefers milk chocolate and has green eyes.
(1.5 marks)

vi) Prefers white chocolate and has green eyes.
(1.5 marks)

vii) Prefers plain chocolate and has blue eyes.
(1.5 marks)

viii) Prefers milk chocolate and has blue eyes.
(1.5 marks)

ix) Prefers white chocolate and has blue eyes.
(1.5 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – May 2017 – L1 – Q6a – Probability"

  • 9 Marks

QT – Nov 2016 – L1 – Q1b – Probability

This part focuses on calculating the probability of an ICAG-qualified individual and their spouse being selected for a position.

Mr. Agbagba, an ICAG qualified member, and his wife, an ICAEW qualified member, attended an interview for two vacancies for the post of College Finance Officer at a Private University. The probability of the interview panel selecting the man is 1/7, and that of the wife is 1/5.

Required:
Assuming the event of selecting a man and selecting a woman are independent, determine the probability that:
i) Both of them will be selected. (3 marks)
ii) Only one of them will be selected. (3 marks)
iii) None of them will be selected. (3 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – Nov 2016 – L1 – Q1b – Probability"

  • 6 Marks

QT – Nov 2016 – L1 – Q1a – Probability

Explains key probability terms such as independent events, mutually exclusive events, and joint probability.

Distinguish between the following terms as used in probability:
i) Independent Events and Dependent Events. (2 marks)
ii) Mutually exclusive Events and Exhaustive Events. (2 marks)
iii) Marginal Probability and Joint Probability. (2 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – Nov 2016 – L1 – Q1a – Probability"

  • 20 Marks

QT – Nov 2018 – L1 – Q7 – Probability

Calculate expected returns for investments, determine optimal strategy, and analyze student error distribution.

Royal Driving School is considering investing in a profitable project. The school is given the following investment alternatives and percentage rates of return.

Over the past 300 days, market conditions have been moderate for 150 days and good for 60 days.

Required:
i) Calculate the expected return for each type of investment. (4 marks)
ii) Determine the optimum investment strategy for Royal Driving School. (3 marks)

b) The number of errors made by 294 students of Royal Driving School in their first attempt at a driving test is grouped in the following frequency distribution:

Number of Errors Number of Students
7 – 13 3
14 – 20 12
21 – 27 23
28 – 34 44
35 – 41 54
42 – 48 56
49 – 55 43
56 – 62 24
63 – 69 23
70 – 76 12

Required:
i) Compute an estimate of the mean and mode for the distribution. (3 marks)
ii) Construct an ogive for the distribution. (4 marks)
iii) Using the ogive in (ii) above, estimate the median for the distribution. (3 marks)
iv) Use the ogive in (ii) above to estimate the percentage of errors within one standard deviation of the mean. (3 marks)

Login or create a free account to see answers

Login
Register

Find Related Questions by Tags, levels, etc.

Report an error
Report an error

You're reporting an error for "QT – Nov 2018 – L1 – Q7 – Probability"

Elevate your professional expertise across key business domains with our comprehensive training programs

Our offerings

Contact Info

  • +233203701923
    +233543919232
  • info@knowsia.com

Customer

Get In Touch

Follow us on our social media and get daily updates.

Facebook-f Twitter Linkedin-in Envelope
Oops!

This feature is only available in selected plans.

Click here to view all plans

Click on the login button below to login if you’re already subscribed to a plan or click on the upgrade button below to upgrade your current plan.

Login
Upgrade Plan

If you’re not subscribed to a plan, click on the button below to choose a plan

Subscribe to a plan